刷题使我快乐,满脸开心.jpg
- 来源:力扣(LeetCode)
- 链接:https://leetcode.cn/problems/trapping-rain-water/
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
思路
首先,强推这篇题解,五种解法层层递进,受益匪浅:五种解法精选题解
我个人解法是‘解法三’,优先说下这种解法的思路:
首先在基本思路上,是逐列的去求雨水量,而我们根据木桶原理的思维,很容易就能明白,每一列的水量,取决于这一列的左边最大值,和右边最大值的较小值。这个左最大值和右最大值是随着位置不断变化的,那么每次遍历到一个位置,再去起循环求两边最大值肯定是时间复杂度高多了(对应上文题解第二种解法),所以,可以先预处理走两趟数组,求出每个位置的左最大值和右最大值
这样在遍历到每个位置时候,就不需要单独去求了, 直接取用即可。
再进一步优化空间复杂度就是‘解法四’
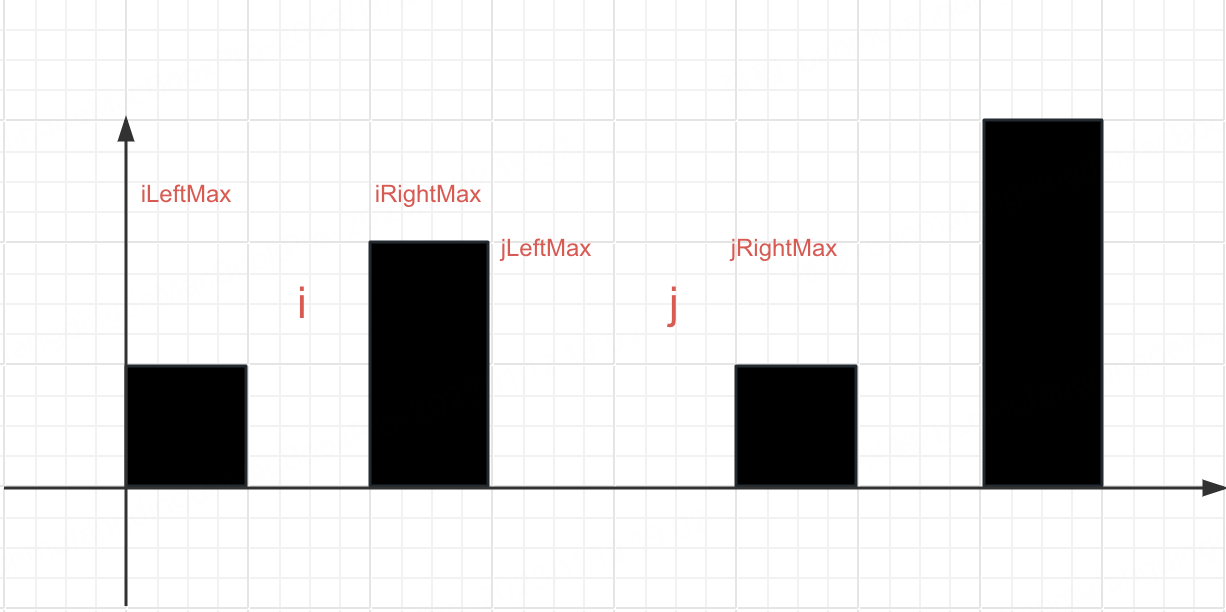
这里有一个数学推理,如下图所示:
i位置的水量取决于iLeftMax和iRightMax,
j位置的水量取决于jLeftMax和jRightMax。
而iRightMax正常应该是从右往左一步步比大小得到的,所以
式一:
iRightMax >= jRightMax,
同理
式二:jLeftMax >= iLeftMax
所以‘解法四’所谓双指针法就是
- 卡住
i位置和j位置的左右两边 - 当
iLeftMax大于jRightMax时,根据式二,可得jLeftMax >= (iLeftMax >=) jRightMax,所以我们可以只根据jRightMax计算j位置水量。然后i位置右移,更新iLeftMax继续求解 - 同理,
iLeftMax小于jRightMax时,根据式一,可得iRightMax >= (jRightMax >=) iLeftMax,所以我们可以只根据iLeftMax计算i位置水量。然后j位置左移,更新jRightMax继续求解
之所以这么大费周章,就是因为如果要两边都求解卡住,则因为最终遍历时只能照顾一边,所以另一边必须要做存储,空间复杂度无法降低。
栈思路也是比较直接,但代码却要注意些细节
感兴趣可以自行看题解或者尝试下~
至此,上代码
代码
时间复杂度O(n)。空间复杂度O(n)
func trap(height []int) int {
n := len(height)
// 求出中间各位置的左边最大值
maxLeft := make([]int, n)
for i:=1; i<=n-2; i++ {
if height[i-1] > maxLeft[i-1] {
maxLeft[i] = height[i-1]
} else {
maxLeft[i] = maxLeft[i-1]
}
}
// 求出中间各位置的右边最大值
maxRight := make([]int, n)
for i := n-2; i>=0; i-- {
if height[i+1] > maxRight[i+1] {
maxRight[i] = height[i+1]
} else {
maxRight[i] = maxRight[i+1]
}
}
// 根据左右最大边界得出每一列水量
sum := 0
for i:=1; i<= n-2;i++ {
min := maxLeft[i]
if min > maxRight[i] {
min = maxRight[i]
}
if min > height[i] {
sum += min - height[i]
}
}
return sum
}
时间复杂度O(n)。空间复杂度O(1)
func trap(height []int) int {
n := len(height)
// 0和n-1边界不可能有水
i := 1
j := n-2
// 由思路可知,其实只用i位置左最大值,j位置右最大值即可
iLeftMax := 0
jRightMax := 0
sum := 0
for i <= j {
if iLeftMax < height[i-1] {
iLeftMax = height[i-1]
}
if jRightMax < height[j+1] {
jRightMax = height[j+1]
}
// 情况1,我们求j位置的水
if iLeftMax > jRightMax {
if jRightMax > height[j] {
sum += jRightMax - height[j]
}
j--
// 情况2,我们求i位置的水
} else {
if iLeftMax > height[i] {
sum += iLeftMax - height[i]
}
i++
}
}
return sum
}