刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/maximal-square/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

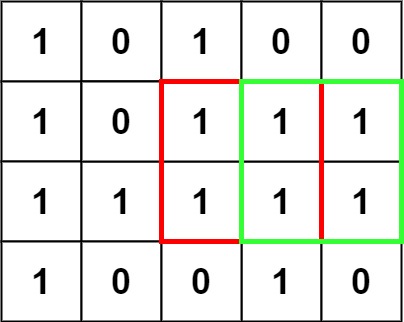
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

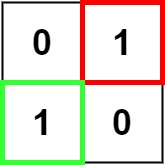
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 '0' 或 '1'

思路

暴力法肯定是可以的，但是无论怎么剪枝，复杂度都很难降低到一个比较满意的程度。所以当时就想到，如果用动态规划可不可行呢？

1. dp[i][j]的含义还是比较简单的，即以此坐标为左上角的正方形的最大边长
2. 初始化，对于每个格子，是0则肯定不会是成正方形，所以是0，如果是1那么起码会是一个1边长的正方形。
3. 剩下就是最容易卡住的状态转移方程了
   不过其实可以通过一个图来得出来一个状态转移方程：
   

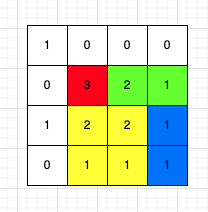
在红色[i][j]位置，其边长会根据[i-1][j]、[i][j-1]、[i-1][j-1] 三个位置的边长来表示，因为这三个位置形成的正方形，如果边长都相等时，那么加上[i][j]为1则就能正好的拼出一个更大边长的正方形来。相对的，如果某一块边长较短，那么就只能取其最小的边长+1了。

所以状态转移方程就是：

dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1

至此，上代码

代码

func maximalSquare(matrix [][]byte) int {
	m := len(matrix)
	n := len(matrix[0])

	res := 0
	// dp[i][j] 的含义是以此坐标为左上角的正方形的最大边长
	dp := make([][]int, m)
	// 初始化数据
	for i, _ := range dp {
		dp[i] = make([]int, n)
		for j, _ := range dp[i] {
			dp[i][j] = int(matrix[i][j] - '0')
			if dp[i][j] == 1 && res == 0 {
				res = 1
			}
		}
	}
    // 不为‘0’才可能凑成正方形
	for i := m - 2; i >= 0; i-- {
		for j := n - 2; j >= 0; j-- {
			if dp[i][j] == 1 {
				dp[i][j] = min(min(dp[i+1][j], dp[i][j+1]), dp[i+1][j+1]) + 1
			}
			if dp[i][j] > res {
				res = dp[i][j]
			}
		}
	}
    // 需要返回的是面积
	return res * res
}