刷题使我快乐,满脸开心.jpg
- 来源:力扣(LeetCode)
- 链接:https://leetcode.cn/problems/ugly-number-iii/
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目
给你四个整数:n 、a 、b 、c ,请你设计一个算法来找出第 n 个丑数。
丑数是可以被 a 或 b 或 c 整除的 正整数 。
示例 1:
输入:n = 3, a = 2, b = 3, c = 5
输出:4
解释:丑数序列为 2, 3, 4, 5, 6, 8, 9, 10... 其中第 3 个是 4。
示例 2:
输入:n = 4, a = 2, b = 3, c = 4
输出:6
解释:丑数序列为 2, 3, 4, 6, 8, 9, 10, 12... 其中第 4 个是 6。
示例 3:
输入:n = 5, a = 2, b = 11, c = 13
输出:10
解释:丑数序列为 2, 4, 6, 8, 10, 11, 12, 13... 其中第 5 个是 10。
示例 4:
输入:n = 1000000000, a = 2, b = 217983653, c = 336916467
输出:1999999984
提示:
1 <= n, a, b, c <= 10^9
1 <= a * b * c <= 10^18
本题结果在 [1, 2 * 10^9] 的范围内
思路
这道题看似跟前面两道丑数题大差不差,但其实因为此题中,丑数是可以被a 、b 、c整除,而不是仅能被a 、b 、c整除,导致了其实跟强两道题相去略远,况且题中其实有个隐含条件,如果还按照队列方式一个个找出第n个丑数,会OOM,所以此题需要转换思路。
解题思路如下
1、首先,就是丑数是可以被a 、b 、c整除的数字,所以对于一个数字来说,小于等于此数字的丑数个数是可以被计算出来的。这里用到的是容斥定理。
(A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C)
即:
丑数个数 = 能被a分别整除的数字个数 + 能被b分别整除的数字个数 + 能被c分别整除的数字个数 - 能被a和b都整除的数字个数 - 能被a和c都整除的数字个数 - 能被b和c都整除的数字个数 + 能被a和b和c都整除的数字个数
直观图如下:
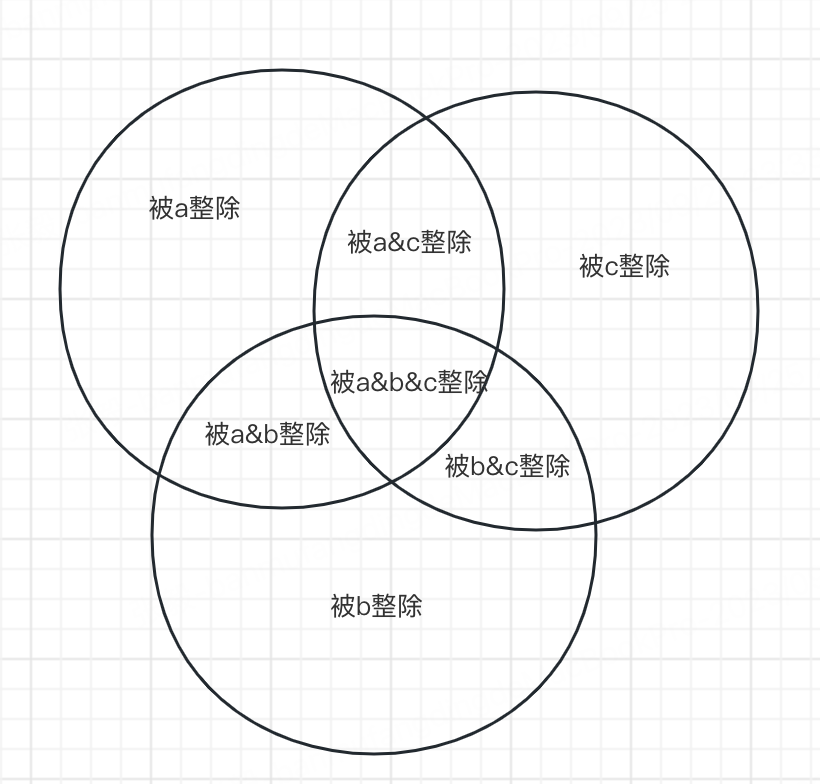
2、其次,当得知丑数可以被计算出来之后,我们由之前的队列思维,可以小于等于某一个数字的丑数个数肯定跟这个数字的大小是正相关的,所以就可以通过二分法来逐步确认第n个丑数是哪个数字
剩下的就是容斥定理的带入求解方式了,这里会用到的就是,最大公约数求法:
func gcm(a, b int) int {
for a != 0 {
a, b = b%a, a
}
return b
}
以及最小公倍数求法,如此就可以求解给定数字内,同时被多个因数整除的数字个数了
func lcm(a, b int) int {
return a * b / gcm(a, b)
}
代码
func nthUglyNumber(n int, a int, b int, c int) int {
lcm_ab, lcm_bc, lcm_ac := lcm(a, b), lcm(b, c), lcm(a, c)
lcm_abc := lcm(a, lcm_bc)
floor, ceil := 0, min(min(a, b), c) * n
for floor <= ceil {
mid := (floor + ceil) / 2
num := mid/a + mid/b + mid/c - mid/lcm_ab - mid/lcm_bc - mid/lcm_ac + mid/lcm_abc
if num == n {
if mid%a == 0 || mid%b == 0 || mid%c == 0 {
return mid
} else {
ceil = mid - 1
}
} else if num > n {
ceil = mid - 1
} else {
floor = mid + 1
}
}
return floor
}
func lcm(a, b int) int {
return a * b / gcm(a, b)
}
func gcm(a, b int) int {
for a != 0 {
a, b = b%a, a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}