刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/rotate-image/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

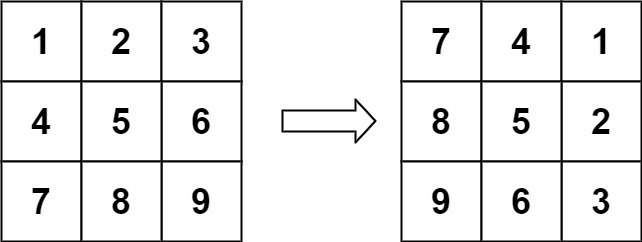
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

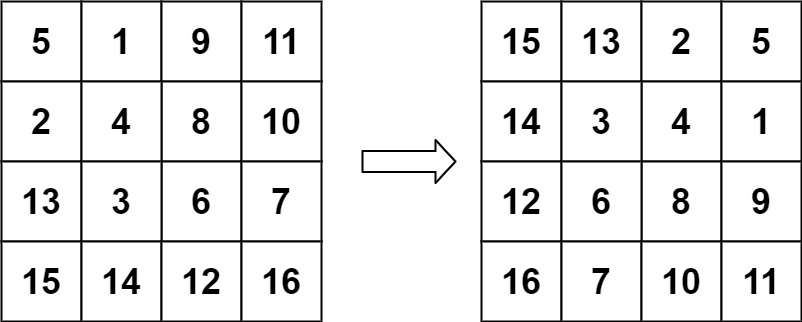
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

思路

我的思路比较原始，就是既然是要转，那总归会有一个转的规律，那从题中可以看出：

每一层进行一个90度旋转之后，其实每个数据将要旋转到的位置其实是可以用层和层内坐标来描述的

如下图：

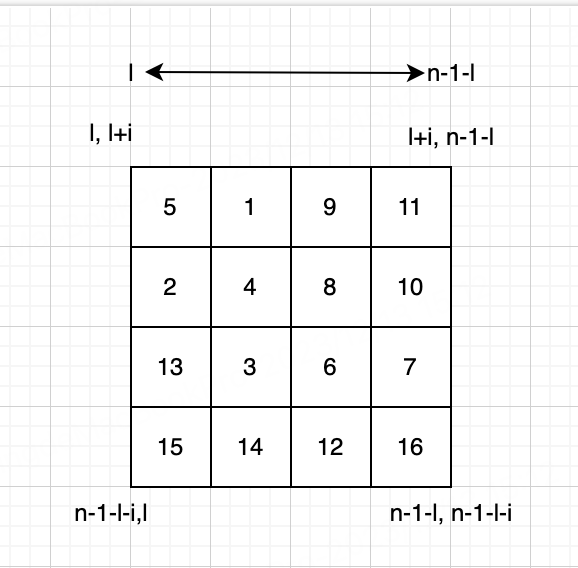
以第一层为例，每个数据旋转后的位置可以如下表示(l为层数，i为层内坐标)：

• [l][l+i] -> [l+i][n-1-l]
• [l+i][n-1-l] -> [n-1-l][n-1-l-i]
• [n-1-l][n-1-l-i] -> [n-1-l-i][l]
• [n-1-l-i][l] -> [l][l+i]

这里i用的是一维数组的下标，用二维数组下标同理

这样描述出来之后，剩下就是层和层内坐标的遍历了：

• 首先是层数，这里易得，需要 l < n/2
• 至于层内坐标，这里其实最大的限制就是，当前层倒数第一个元素是不需要遍历到的，因为它本身就是当前层一个元素将要到达的位置

那么基本上代码就出来了，上代码

代码

func rotate(matrix [][]int) {
    // 特殊情况快速返回
	if len(matrix) == 1 {
		return
	}
	n := len(matrix)
    // 遍历层
	for l := 0; l < n/2; l++ {
        // 遍历层内坐标
		for i := 0; l+i < n-l-1; i++ {
            // 按旋转顺序移动数据
			matrix[l][l+i], matrix[l+i][n-1-l], matrix[n-1-l][n-1-l-i], matrix[n-1-l-i][l] =
				matrix[n-1-l-i][l], matrix[l][l+i], matrix[l+i][n-1-l], matrix[n-1-l][n-1-l-i]
		}
	}
}