刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/powx-n/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，x^n ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

• -100.0 < x < 100.0
• -2^31 <= n <= 2^31-1
• n 是一个整数
• 要么 x 不为零，要么 n > 0 。
• -10^4 <= x^n <= 10^4

思路

没思路不大可能，一个个乘就完了，顶多注意下负数的次幂。

不过不优化的话，这个题就太简单了

而既然嫌一个个乘太慢，那就加快乘的速度，如图所示：

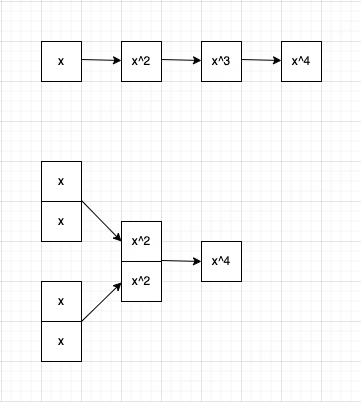
同样是四个x相乘，利用二分之后得到的中间结果参与计算，就会减少所需要计算的步骤了

基本上思路就是如此，直接上代码，细节在注释

官方题解中还有空间复杂度更低的迭代思路，可以移步学习~

代码

func myPow(x float64, n int) float64 {
    // 任何数0次幂都是1，快速返回
	if n == 0 {
		return 1
	} else if n > 0 {
		return mul(x, n)
	} else {
        // 负数次幂需要注意
		return 1.0 / mul(x, -n)
	}
}

func mul(x float64, n int) float64 {
    // 递归的返回点
	if n == 0 {
		return 1
	}
    // x2即是中间结果了，利用它可以更快完成计算
	x2 := mul(x, n/2)
	if n%2 == 1 {
		return x2 * x2 * x
	} else {
		return x2 * x2
	}
}