刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/validate-binary-search-tree/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

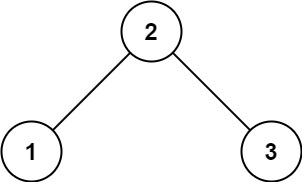
输入：root = [2,1,3]
输出：true

示例 2：

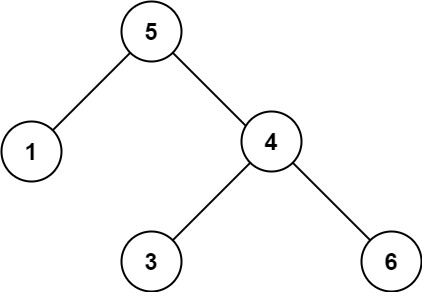
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -2^31 <= Node.val <= 2^31 - 1

思路

思路应该还是比较简单的，在DFS的基础上改动一下就可以：

• 需要判断当前节点是否满足条件，即左子节点比根节点大，右子节点则需要比根节点小
• 并且，需要让其左子节点都比自己小，右子节点则都比自己大

直接上代码

代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isValidBST(root *TreeNode) bool {
    // 先根据题目备注圈一个一定符合的范围
    return isBST(root, math.MaxInt, math.MinInt)
}

func isBST(root *TreeNode, max, min int) bool {
    if root == nil {
        return true
    }
    if root.Val <= min || root.Val >= max {
        return false
    }
    // 父节点对于子节点的影响是单方向的
    return isBST(root.Left, root.Val, min) && isBST(root.Right, max, root.Val)
}