刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/maximum-sum-circular-subarray
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给定一个长度为 n 的环形整数数组 nums ，返回 nums 的非空 子数组 的最大可能和 。

环形数组 意味着数组的末端将会与开头相连呈环状。形式上， nums[i] 的下一个元素是 nums[(i + 1) % n] ， nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。

子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上，对于子数组 nums[i], nums[i + 1], ..., nums[j] ，不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。

示例 1：

输入：nums = [1,-2,3,-2]
输出：3
解释：从子数组 [3] 得到最大和 3

示例 2：

输入：nums = [5,-3,5]
输出：10
解释：从子数组 [5,5] 得到最大和 5 + 5 = 10

示例 3：

输入：nums = [3,-2,2,-3]
输出：3
解释：从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3

提示：

• n == nums.length
• 1 <= n <= 3 * 104
• -3 * 104 <= nums[i] <= 3 * 104​​​​​​​

思路

可能做过动规里最大子数组合的童鞋应该很快就能想到类似的思路，只要在处理到结尾的时候别忘了是环形数组，可以从头继续接续，另外注意不可重复累加元素的限制条件即可。但是这里不提这个常规思路，介绍一个题解里看到的更牛的思路：

题解链接：戳

思路出处：戳
这里只盗张图，然后就不赘述一遍了，题解说的已经很是详尽了

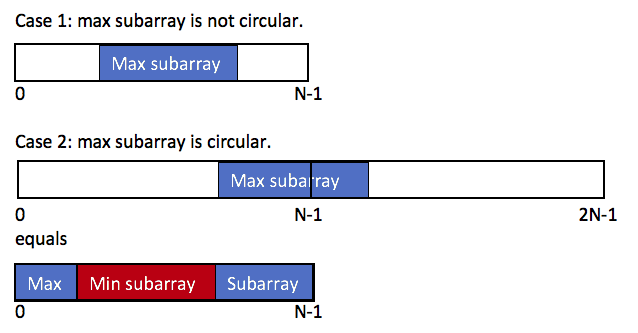
代码

func maxSubarraySumCircular(nums []int) int {
    total, maxSum, minSum, currMax, currMin := nums[0], nums[0], nums[0], nums[0], nums[0]

    for i := 1; i < len(nums); i++ {
        total += nums[i]
        currMax = max(currMax+nums[i], nums[i])
        maxSum  = max(maxSum, currMax)
        currMin = min(currMin+nums[i], nums[i])
        minSum  = min(minSum, currMin)
    }

    //等价于if maxSum < 0
    if total == minSum  {
        return maxSum
    } else {
        return max(maxSum, total - minSum)
    }
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}