刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/minimum-path-sum/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

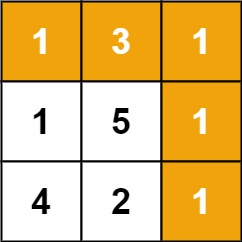
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 200

思路

这道题是道非常标准的动态规划题了

dp[i][j]含义就是到达此位置时的最小路径和

状态方程也很是好写

dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grip[i][j]

还有最后一个问题就是初始化，我们配合一个图来看下：

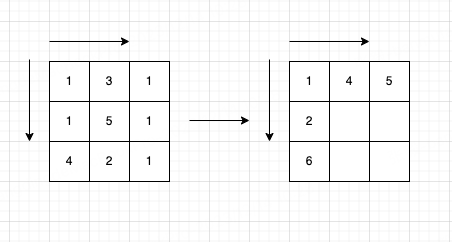
因为只能往下、往右走，那么没有上面元素的第一排，和没有左边元素的第一列，就是可以固定写出对应dp数组内容的地方了，初始化至此也就完成了，其余的元素，其上方和左方元素都可以推算而出了

基本上代码也就出来了

代码

func minPathSum(grid [][]int) int {
	m := len(grid)
	n := len(grid[0])

	// 初始化dp数组
	dp := make([][]int, m)
	for k, _ := range dp {
		dp[k] = make([]int, n)
		// 初始化第一排
		if k == 0 {
			for l, _ := range dp[k] {
				if l == 0 {
					dp[k][l] = grid[k][l]
				} else {
					dp[k][l] = grid[k][l] + dp[k][l-1]
				}
			}
		} else {
			// 初始化第一列
			dp[k][0] = grid[k][0] + dp[k-1][0]
		}
	}

	// 求解
    // 也可以把初始化和后续位置求解放到一个循环，但是感觉这样会更清晰些
	for i := 1; i < m; i++ {
		for j := 1; j < n; j++ {
			dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
		}
	}
	return dp[m-1][n-1]
}

func min(a, b int) int {
	if a > b {
		return b
	}
	return a
}