刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/maximal-rectangle/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：

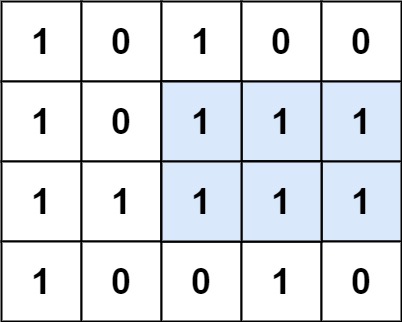
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = [["0"]]
输出：0

示例 3：

输入：matrix = [["1"]]
输出：1

提示：

• rows == matrix.length
• cols == matrix[0].length
• 1 <= row, cols <= 200
• matrix[i][j] 为 '0' 或 '1'

思路

这个问题单独看确实挺困难的，但是如果有了 84题 的 单调栈 思路基础，那就很简单了

LeetCode-84. 柱状图中最大的矩形

无非就是把矩形拆解为一个个柱状图，分别求得最大面积，做一个比较即可：

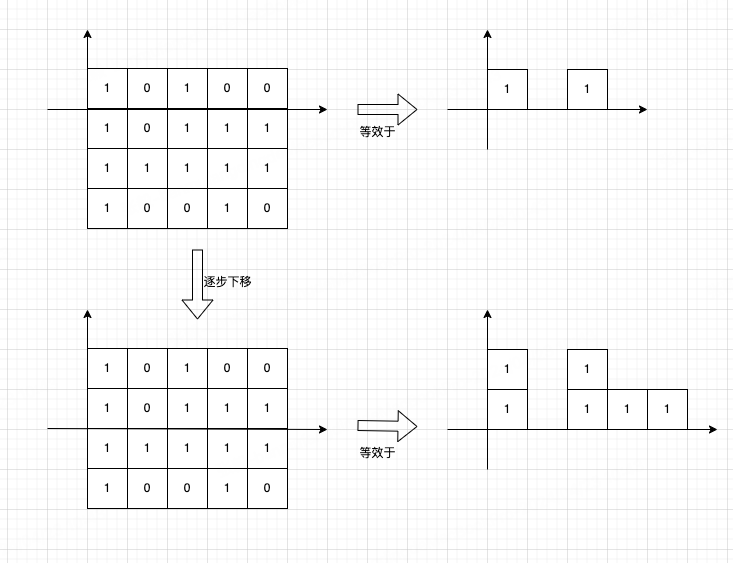
而求最大面积的思路请参考84题，这里就不做赘述了

思路大体就是这样了，细节在注释～

代码

func maximalRectangle(matrix [][]byte) int {
	heights := make([]int, len(matrix[0]))
	res := 0
    // 一层层形成柱状图
    // heights 没有必要定义多个数组，可以重复利用
	for i := 0; i < len(matrix); i++ {
		for j := 0; j < len(matrix[0]); j++ {
			if matrix[i][j] == '1' {
				heights[j]++
			} else {
				heights[j] = 0
			}
		}
		res = max(res, largestRectangleArea(heights))
	}
	return res
}

func largestRectangleArea(heights []int) int {
	n := len(heights)
	// 对于每个高度来说，找到能不低于当前高度的左右边界时，就可以求的此高度下的最大面积了
	// 初始化左右边界数据
	left := make([]int, n)
	right := make([]int, n)
	// 初始化左右边界数据，当数据在 heights数组中 最终找不到边界时，初始化值就是其左右边界了
	for i := 0; i < n; i++ {
		left[i] = -1
		right[i] = n
	}

	pointStack := []int{}
	for i := 0; i < n; i++ {
		// 如果 栈顶元素对应高度 大于 当前元素对应高度，那么 当前元素 就是 栈顶元素 的右边界
		// 参考图一
		for len(pointStack) > 0 && heights[i] <= heights[pointStack[len(pointStack)-1]] {
			right[pointStack[len(pointStack)-1]] = i
			pointStack = pointStack[:len(pointStack)-1]
		}
		// 弹出完毕后 栈顶元素对应高度 小于 当前元素对应高度，那么 栈顶元素 就是 当前元素 的左边界
		// 参考图二
		if len(pointStack) > 0 {
			left[i] = pointStack[len(pointStack)-1]
		}
		// 当前元素 处理完毕，入栈处理下一个元素
		pointStack = append(pointStack, i)
	}
	res := 0
	for i := 0; i < n; i++ {
		// 底边长 不包含左右边界本身，所以需要 再减1
		res = max(res, (right[i]-left[i]-1)*heights[i])
	}
	return res
}