刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/maximum-square-area-by-removing-fences-from-a-field/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

有一个大型的 (m - 1) x (n - 1) 矩形田地，其两个对角分别是 (1, 1) 和 (m, n)，田地内部有一些水平栅栏和垂直栅栏，分别由数组 hFences 和 vFences 给出。

水平栅栏为坐标 (hFences[i], 1) 到 (hFences[i], n)，垂直栅栏为坐标 (1, vFences[i]) 到 (m, vFences[i]) 。

返回通过 移除 一些栅栏（可能不移除）所能形成的最大面积的 正方形 田地的面积，或者如果无法形成正方形田地则返回 -1。

由于答案可能很大，所以请返回结果对 10^9 + 7 取余 后的值。

注意：田地外围两个水平栅栏（坐标 (1, 1) 到 (1, n) 和坐标 (m, 1) 到 (m, n) ）以及两个垂直栅栏（坐标 (1, 1) 到 (m, 1) 和坐标 (1, n) 到 (m, n) ）所包围。这些栅栏 不能 被移除。

示例 1：

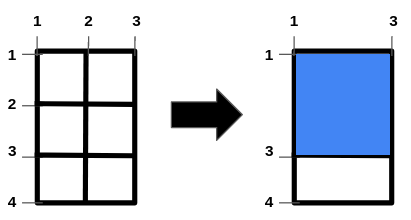
输入：m = 4, n = 3, hFences = [2,3], vFences = [2]
输出：4
解释：移除位于 2 的水平栅栏和位于 2 的垂直栅栏将得到一个面积为 4 的正方形田地。

示例 2：

输入：m = 6, n = 7, hFences = [2], vFences = [4]
输出：-1
解释：可以证明无法通过移除栅栏形成正方形田地。

提示：

• 3 <= m, n <= 10^9
• 1 <= hFences.length, vFences.length <= 600
• 1 < hFences[i] < m
• 1 < vFences[i] < n
• hFences 和 vFences 中的元素是唯一的。

思路

我这里是直接暴力处理了，计算出所有的可能横边长，和所有的竖边长，有相等的，那就是有正方形，取最大的就好

其实就是注意所有横向坐标之间的两两差值，竖向同理
需要注意的就是别忘了初始两个坐标

剩下的就简单了。老样子，细节在代码注释

代码

func maximizeSquareArea(m int, n int, hFences []int, vFences []int) int {
	hSizes := make(map[int]bool, 0)
	hFences = append(hFences, []int{1, m}...)
    // 排个序规避负值问题
	sort.Ints(hFences)
	for i := len(hFences) - 1; i >= 0; i-- {
        // 规避0边长
		for j := i - 1; j >= 0; j-- {
			hSizes[hFences[i]-hFences[j]] = true
		}
	}

	vSizes := make(map[int]bool, 0)
	vFences = append(vFences, []int{1, n}...)
    // 排个序规避负值问题
	sort.Ints(vFences)
	for i := len(vFences) - 1; i >= 0; i-- {
        // 规避0边长
		for j := i - 1; j >= 0; j-- {
			vSizes[vFences[i]-vFences[j]] = true
		}
	}

	maxSize := 0
    // 找出来最长的边长
	for k, _ := range hSizes {
		if _, ok := vSizes[k]; ok {
			if k > maxSize {
				maxSize = k
			}
		}
	}
    // 没有就-1
	if maxSize == 0 {
		return -1
	}
    // 有就计算下
	return (maxSize * maxSize) % int(math.Pow(10, 9) + 7)
}