刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/edit-distance/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

提示：

• 0 <= word1.length, word2.length <= 500
• word1 和 word2 由小写英文字母组成

思路

这道题可能很多人都会想到用动态规划，而且应该也能想到从短到长去切分问题，但是关键在于，如何设定状态转移方程呢？
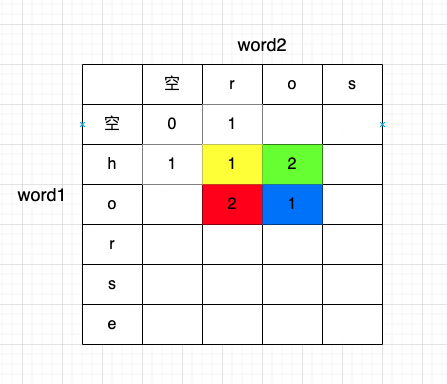
如图，我们按照从短到长的思路，将dp数组含义设计为从word1到word2变换所需步数的一个二维数组。 word1 和 word2 都会有 0、1...len-1、len 这些个位置，此时 dp[i][j]的含义就是

从 i 个长度的 word1 变换到 j 长度的 word2 所需要的步数

这里我们先看两个特殊情况：

• word1 为空时，对应这一行的含义其实就是，一个空字符串变到 word2 所需的步数，自然就是逐个字符增加即可
• word2 为空时，对应这一行的含义其实就是，一个字符串变到 空字符串 所需的步数，其实就是逐个字符删除即可

有了这两个特殊情况，我们的dp数组的初始化其实也就完成了

但是要写出状态转移方程，还是得看图中黄红绿蓝四种情况：

• 黄色位置含义是从h 到 r 所需要变换的次数，我们知道这俩不相等，那就是需要做一次替换即可
• 红色位置含义是从ho 到 r 所需要变换的次数，而我们其实知道了，黄色位置从 h 到 r只需要一次替换，那么我只需要在黄色位置的基础上，多做一次删除操作即可

即，dp[i][j] = dp[i-1][j] + 1

• 再看绿色位置，同理的，从h 到 ro 所需要变换的次数，其实就是在黄色位置的基础上，多做一次插入操作即可

即，dp[i][j] = dp[i][j-1] + 1

• 蓝色位置同理，正常来讲，应该是在黄色位置的基础上，多做一次替换操作了。但此时是从ho 变换到 ro，两者在第二位上对应的字符相同，所以根本不需要再做替换了。

即，正常是 dp[i][j] = dp[i-1][j-1] + 1。 但是字符相同时，dp[i][j] = dp[i-1][j-1]

然后这里还有一个小优化，通过刚才的过程分析，我们很清楚红、绿两个位置都是在黄色基础上增加操作来完成的，所以一旦蓝色位置这种字符相等的情况发生，那么其实蓝色位置的最小次数一定就是黄色位置的次数，不需要再比较三种正常方式的次数然后做选择了

至此，状态转移方程也就有了

上代码

代码

func minDistance(word1 string, word2 string) int {
    n1, n2 := len(word1), len(word2)
    
    // dp[i][j] 意为从 word1 的前`i`个字符串
    // 转变成 word2 的前 `j` 个字符所需要的最少次数
    dp := make([][]int, n1 + 1)
    // 当j为0，意味着从空的 word1 一步步变成 word2 的次数
    // 每个 word2 的字符位置增加一个字符即可
    for i, _ := range dp {
        dp[i] = make([]int, n2 + 1)
        dp[i][0] = i
    }
    // 当i为0，意味着从 word1 一步步变成空的 word2 所需的次数，
    // 同样的，每个 word1 的字符位置删除一个字符即可
    for j, _ := range dp[0] {
        dp[0][j] = j
    }

    for i:=1; i <= n1; i++ {
        for j:=1; j <= n2; j++ {
            if word1[i-1] != word2[j-1] {
                dp[i][j] = min(dp[i][j-1]/*插入*/, min(dp[i-1][j]/*删除*/, dp[i-1][j-1]/*替换*/)) + 1
            } else {
                dp[i][j] = dp[i-1][j-1]
            }
        }
    }
    return dp[n1][n2]
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}