刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/search-in-rotated-sorted-array/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

提示：

• 1 <= nums.length <= 5000
• -104 <= nums[i] <= 104
• nums 中的每个值都 独一无二
• 题目数据保证 nums 在预先未知的某个下标上进行了旋转
• -104 <= target <= 104

思路

首先注意到的是，需要保证O(log n)复杂度，再加上数组基本有序，最直观的思路，就是分治。

整理下现有条件，数组虽然分成了两节，但至少在每一节内有序，可以分情况讨论下在取定左右边界及中值时，各种可能性：

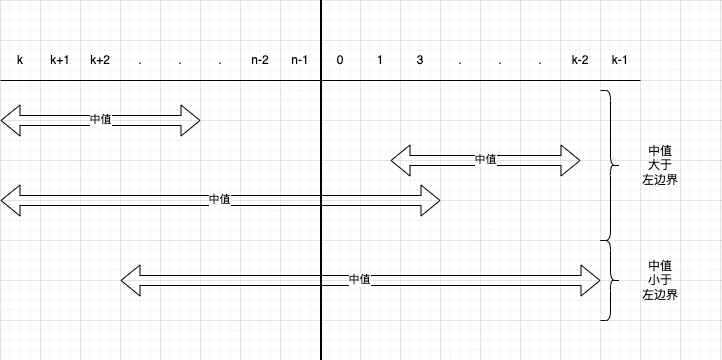
先确定旋转点在哪里

如果中值大于左边界

由图中可以看出

• 如果目标值大于中值，那么目标值一定在右半边
• 如果目标值小于中值，且目标值大于等于左边界时，则在左半边
• 如果目标值小于中值，且目标值小于左边界时，则在右半边

如果中值小于左边界

• 如果目标值小于中值，那么目标值一定在左半边
• 如果目标值大于中值，且目标值大于等于左边界时，则在左半边
• 如果目标值大于中值，且目标值小于左边界时，则在右半边

那如此，二分法代码也就出来了

代码

func search(nums []int, targetNum int) int {
    if len(nums) <= 0 {
        return -1
    }

    leftIndex := 0
    rightIndex := len(nums) - 1
    midIndex := 0

    for leftIndex <= rightIndex {
        midIndex = (leftIndex + rightIndex) / 2
        if nums[midIndex] == targetNum {
            return midIndex
        }

        if nums[midIndex] >= nums[leftIndex] {
            // 边界判断target在哪个区间
            if nums[midIndex] > targetNum && nums[leftIndex] <= targetNum {
                rightIndex = midIndex - 1
            } else {
                leftIndex = midIndex + 1
            }
        } else {
            if nums[midIndex] < targetNum && nums[leftIndex] > targetNum {
                leftIndex = midIndex + 1
            } else {
                rightIndex = midIndex - 1
            }
        }
    }

    return -1
}