刷题使我快乐,满脸开心.jpg
- 来源:力扣(LeetCode)
- 链接:https://leetcode.cn/problems/sliding-window-maximum/
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
思路
感觉一涉及到单调栈、单调队列这种,很容易就标上一个困难。想了下原因,可能是在于这种思维往往需要构造出一个平时难以见到的数据结构,增加了心智负担,所以标为了困难。但是,如果你见多了某种结构,那么至少此种结构便于解决的问题,对你来说就不是一个难题了。这就是所谓的会者不难,难者不会吧。
之前见多了单调栈(感兴趣可以点单调栈标签看看其他题目~),所以开始第一思维就是用单调栈来处理,但是后来实际写代码时候发现(示例1数据为例):
-
如果将值更大的数字放在栈顶,那么在面临新增元素为小值时无法处理后续值变小但是窗口滑动时它们确实需要保留的情况。所以需要将后面的值进行保留,以应对窗口滑动的行为
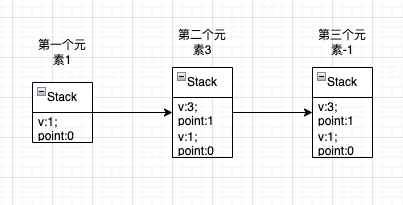
-
所以改了下,将值更大的数字放在栈底,那么会是这种情况,此时其实我们需要的是从栈底取值,所以这已经不是栈了,应该叫队列了:
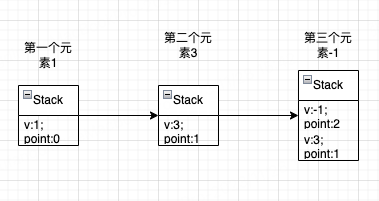
后来看题解,还真的是叫单调队列,那种感觉确实很难言说了,舒爽~哈哈哈
所以,思路整理如下:
- 维护一个队列,按下标从小到大放入元素时,剔除比入队值小的值,没有比入队值小的,则压入队列。因为按下标顺序入队,所以此值肯定比之前的值更晚划出窗口,所以不用担心窗口滑动带来问题。
- 初始时将
k个元素入队列,队首元素就是目前最大的元素了,加入结果集 - 后续开启循环,将一个个后续值入队,均执行
步骤1操作,但随着开始入队后续窗口的值,需要检查队首的下标是否还满足在窗口内,不满足则剔除,直到找到满足在窗口内的新的队首元素,加入结果集 - 遍历完给定数组,结束循环。
至此,上代码。
代码
func maxSlidingWindow(nums []int, k int) []int {
// point query 下标队列
pq := make([]int, 0)
add := func(i int) {
// 队列尾小于此值的均剔除
// 因为下标肯定比此值小,更早划出窗口,所以可以剔除
for len(pq) > 0 && nums[i] >= nums[pq[len(pq)-1]] {
pq = pq[:len(pq)-1]
}
// 此时留下的元素,从队列头到队列尾:值递减,但是下标递增
pq = append(pq, i)
}
// 初始窗口中的值入队列
for i := 0; i < k; i++ {
add(i)
}
n := len(nums)
res := make([]int, 0, n-k+1)
res = append(res, nums[pq[0]])
for i := k; i < n; i++ {
add(i)
// 对于划出窗口的下标,执行剔除
for pq[0] <= i-k {
pq = pq[1:]
}
// 此时队列头就是值最大,下标满足窗口的元素了
res = append(res, nums[pq[0]])
}
return res
}