刷题使我快乐，满脸开心.jpg

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/longest-increasing-path-in-a-matrix/
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

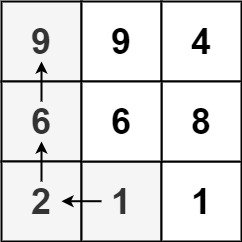
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

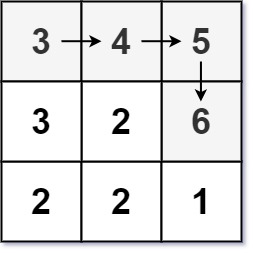
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 2^31 - 1

思路

虽然说是一道困难题，但是思路其实比较简单，记忆化搜索即可

所以更多的是对于记忆化搜索的实现，有一个小tips就是

把每个位置最长路径值至少为1 的 初始化滞后，使得 值为0时 顺便承担 尚未搜索过 的状态

没太多可说的，直接上代码，细节在注释。

代码

func longestIncreasingPath(matrix [][]int) int {
	if len(matrix) == 0 || len(matrix[0]) == 0 {
		return 0
	}

    // 初始化
	m, n := len(matrix), len(matrix[0])
	mem := make([][]int, m)
	for i := range mem {
		mem[i] = make([]int, n)
	}

	var dfs func(i, j int)
	dfs = func(i, j int) {
		if mem[i][j] != 0 {
			return
		}
        // 最小长度为1，不放到初始化是为了上面是否为0的判断
        // 也就是让 “值为0” 承担了 “还没有处理过” 的含义
		mem[i][j] = 1
		for _, direction := range [][]int{{0, 1}, {0, -1}, {1, 0}, {-1, 0}} {
            // 分四个方向进行尝试
			x, y := i+direction[0], j+direction[1]
			if x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] <= matrix[i][j] {
				continue
			}
            // 计算相邻位置的最大长度
			dfs(x, y)
            // 比较取最大值
			mem[i][j] = max(mem[i][j], mem[x][y]+1)
		}
	}
	maxPath := 0
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			dfs(i, j)
            // 尝试更新结果
			if maxPath < mem[i][j] {
				maxPath = mem[i][j]
			}
		}
	}
	return maxPath
}