刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/maximum-width-of-binary-tree/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

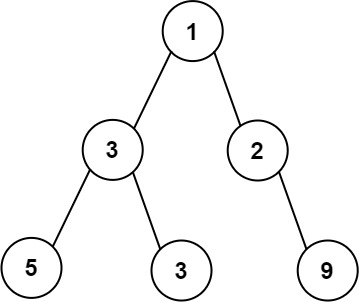
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

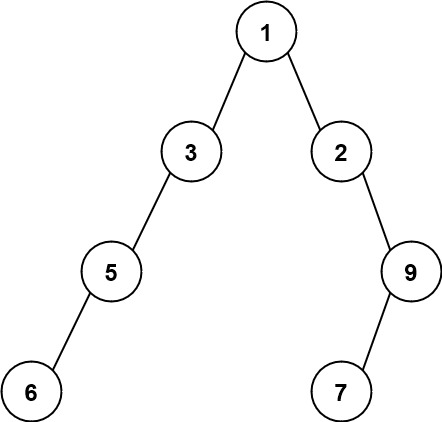
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

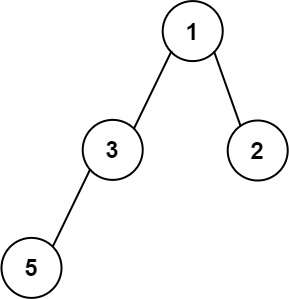
输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

• 树中节点的数目范围是 [1, 3000]
• -100 <= Node.val <= 100

思路

首先是理解题意，这里直白点翻译下最大宽度：

每层中，最左端非空节点和最右端非空节点之间，假设是满二叉树情况下的距离。

要素有两个：

• 最左端非空节点 和 最右端非空节点
• 满二叉树情况下的距离

这里乍一听可能有点思路丢失，但是如果对二叉树特征了解的话

其实满二叉树的情况下，每个节点的下标都是可以根据父节点计算的
也就是说
只要找最左、最右非空节点，每层的宽度就是可计算的

所以问题转变成了

带着父节点的下标寻找最左、最右非空节点

私以为这种情况下

• BFS的心智负担是比较小的，而且复杂度也不会太差
• 带着父节点下标这个问题，构造一个包含节点和对应下标值的结构体就好了~

代码也基本就出来了。老样子，细节在代码注释

代码

type TreeNodeIndex struct {
	Node  *TreeNode
	Index int
}

func widthOfBinaryTree(root *TreeNode) int {
	nodeIdxs := []*TreeNodeIndex{{root, 0}}
	temp := make([]*TreeNodeIndex, 0)
	res := 0
    // 遍历完整棵树的条件
	for len(nodeIdxs) != 0 {
        // 按这里代码的顺序，左节点在前，右节点在后，所以用后面的减前面的
        // 提交时候才发现golang语言里，这个max函数是默认提供的
		res = max(nodeIdxs[len(nodeIdxs)-1].Index-nodeIdxs[0].Index+1, res)
		for _, nodeIdx := range nodeIdxs {
            // 优先放入左节点
			if nodeIdx.Node.Left != nil {
				temp = append(temp, &TreeNodeIndex{
					Node:  nodeIdx.Node.Left,
                    // 左右子节点下标均可计算得出
					Index: 2*nodeIdx.Index + 1,
				})
			}
			if nodeIdx.Node.Right != nil {
				temp = append(temp, &TreeNodeIndex{
					Node:  nodeIdx.Node.Right,
					Index: 2*nodeIdx.Index + 2,
				})
			}
		}
        // 更新每层节点列表
		nodeIdxs = temp
		temp = nil
	}
	return res
}