刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/binary-tree-maximum-path-sum/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其最大路径和。

示例 1：

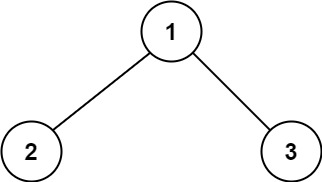
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

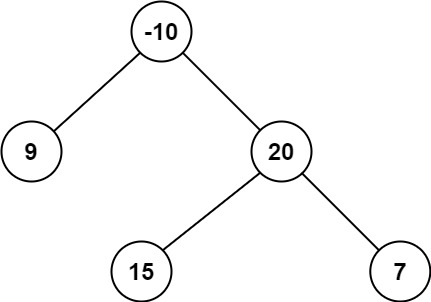
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

• 树中节点数目范围是 [1, 3 * 104]
• -1000 <= Node.val <= 1000

思路

这道题难就难在思路有没有理清楚。

其实对于每个节点，都有几种可能的情况，我们先分别说清楚这些情况：

叶子节点

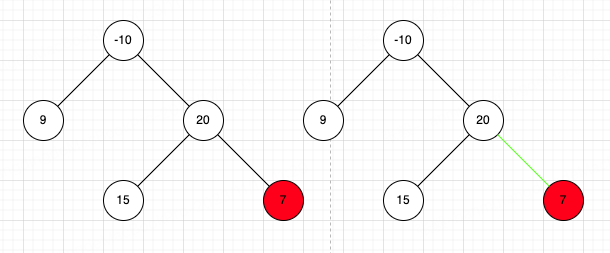
对于叶子节点来说，他们没有子节点（子节点和为0），能出现在结果集的可能情况就是：

• 一种是其父节点经过的所有路径都是负，所以其本身为最大和
• 一种是其父节点的路径中有非负情况，所以其本身为父节点路径中的一部分，姑且称之为给父节点贡献自身的值

根节点

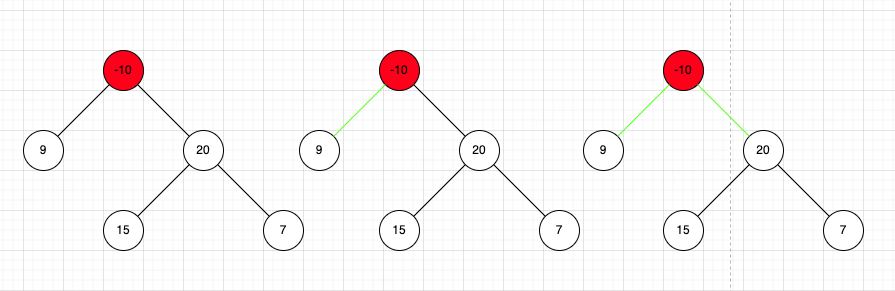
根节点会存在三种情况

• 一种是左右子树均为负，它本身为最大和。根节点就不用考虑父节点的影响了
• 一种是选择左子树或者右子树，此时说明有一条子树和为负数
• 一种是选择左子树和右子树，此时说明左右子树均是正数

中间节点

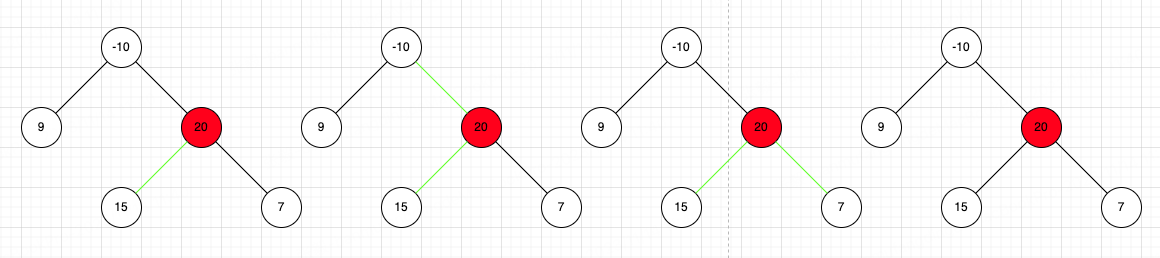
中间节点情况会稍多一些

• 一种是其父节点经过的路径均为负，且左右子树只有一个非负，则只选择左子树或者只选择右子树
• 一种是其父节点经过的路径存在非负，且比左右子树至少其中一方的最大和更大，所以只选择左右子树中较大的一个
• 一种是其父节点经过的路径均为负；或者存在非负，但是都比左右子树的最大和小，且左右子树均非负，则左右子树均选择；又或者只有左右子树其中一个为非负，则只选择一条。
• 最后就是父节点经过的路径、左右子树最大和均为负，只选择节点自身是最大解

总结

到这里我们大致整理了所有节点的所有情况，其实在整理的过程中我们能看到很有情况是可以合并的。大体上来说，其实分为两大类：

• 第一类，是不选择父节点，这时就需要以自身值为基础，整合左右子树的最大和，如果左右子树中最大和为负的则不选择，非负的则纳入。（对于叶子结点来说，相当于左右子树最大和均为0）
• 第二类，是选择父节点，这时就需要以自身值为基础，再去比较左右子树最大和，均为负则均不纳入，否则就选择更大的那个子树最大和纳入，这样得到的结果，就是对父节点最大的贡献。（对于根节点来说，相当于父节点最大和为0）

其实，这样说下来，连编码思维也都出来了，那就是递归，我们一个个子树的深入去求解，不断地根据左右子树最大和的是否非负、选取大小，

• 对于第一类结果，那就是一种路径求解，可以看是否可以刷新最大值
• 对于第二类结果，那就是选择出作为一个子树能给父节点的最大的贡献了，可以作为返回值给到父节点
• 而至于退出条件，那就是走到叶子节点的左右子树时，因为不存在跟值为0是等价的，就可以直接返回0。

大体思路就是如此了，还有一些比较细节的，放到了代码注释，可以看下
至此，上代码

代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
var max int

func maxPathSum(root *TreeNode) int {
  if root == nil {
    return 0
  }
  // 这一行是因为发现LeetCode存在不同用例执行时max值未归零的情况
  max = math.MinInt
  _ = getMaxSum(root)
  return max
}

func getMaxSum(root *TreeNode) int {
  // 叶子节点，对父节点贡献为0
	if root == nil {
		return 0
	}
	// 求得左子树的最大和
    // 对父节点的贡献，肯定为只选取一条子树，但是要注意是否非负
	leftMax := maxInt(0, getMaxSum(root.Left))
	// 求得右子树的最大和
	rightMax := maxInt(0, getMaxSum(root.Right))

	// 左子树和右子树都选取能得到的最大和
	// 此种情况因为无法再链接父节点，所以只是一种情况，也不用返回
    max = maxInt(max, root.Val+leftMax+rightMax)
	
    // 返回选取左子树或者右子树，或者都不选取（此时均为0）的情况
	return root.Val + maxInt(leftMax, rightMax)
}

func maxInt(a, b int) int {
	if a > b {
		return a
	}
	return b
}