刷题使我快乐,满脸开心.jpg
- 来源:力扣(LeetCode)
- 链接:https://leetcode.cn/problems/k-th-smallest-in-lexicographical-order/
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目
给定整数 n 和 k,返回 [1, n] 中字典序第 k 小的数字。
示例 1:
输入: n = 13, k = 2
输出: 10
解释: 字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9],所以第二小的数字是 10。
示例 2:
输入: n = 1, k = 1
输出: 1
提示:
1 <= k <= n <= 10^9
思路
首先得说明下,这道题是道困难题,但别急的划走,字节常考!!!(虽然好像是校招常考)
思路提示
如果你选择了继续留下来看完,那请先看下思路提示,自行写写画画再往下看
- 字典序可以类比十叉树
- 字典序就是十叉树的前序遍历
- 字典序中的第
K个数字也就是前序遍历的第K个数字
思路拆解
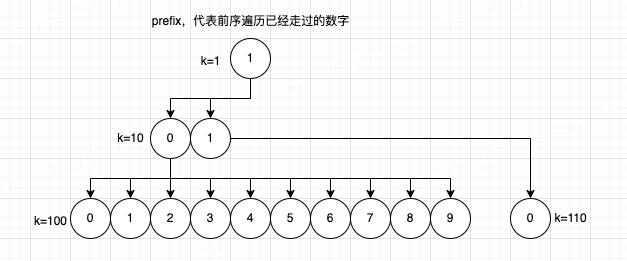
以十叉树类比数字开头的集合
- 其实我们很容易想到先判断
1开头集合个数是否大于n,然后2开头、3开头等等。其实这就类比一个个的十叉树,1开头的树中,所有节点个数也就是1开头集合元素个数 - 确定集合后,继续深入划分一个个小集合,比如
1开头集合中分为- 没有后续节点的集合
1本身 10开头的集合11开头的集合 等等
- 没有后续节点的集合
基于上面的思路我们会产生一个问题,如何把切换集合转变到代码?
可以类比到十叉树去理解:
- 比如当前集合不存在结果,我们需要到下一个集合寻找,那么其实就是从当前的二叉树
右移到下一个节点,也就是数值 + 1 - 比如当前集合存在结果,那我们需要深入到小集合里寻找,那么除了父节点本身的情况,其实就是从
父节点到第一个子节点,也就是数值 * 10(父节点本身的情况我们会在代码里详细说明~)
说完了根据树节点(集合)数量判断移动方法,还有另外一个问题,如何求树节点(集合)数量?
这里类比到十叉树会比较清晰(参考 k=10节点 ):
- 第一层为父节点本身,个数为
1(即节点k=11的值减去k=10节点的值) - 第二层为子节点,个数为
10(右边节点k=11的第一个子节点k=110的值减去k=10节点第一个子节点k=100的值) - 以此类推,从图上很直观的就能看出来节点个数与节点代表的数值的关系,这样也就很容易转换为代码
大体思路就是这样了,那么下面请移步代码,结合注释和十叉树的图,继续深入看实现
PS,暴力排序的路子,据说被用例堵死了
不过真实面试时候可别太较真,想不起来最优解时,先写一个能解决问题的更重要
代码
func findKthNumber(n int, k int) int {
// 请结合十叉树的图来看代码!!!
// 请结合十叉树的图来看代码!!!
// 请结合十叉树的图来看代码!!!
// 求解以prefix为根结点的树的所有节点元素(集合)个数,别忘了有 n 的限制
var getCount = func(prefix int) int {
count := 0
// 这里 root 为根结点含义,可以结合十叉树的图看
// 从根结点这层开始,每次循环都是求下一层节点个数
root := prefix
nextRoot := root + 1
for root <= n {
// 正常 当前层元素个数 nextRoot - root
// 但是 nextRoot>n 时,此层元素并不满,只能计算部分元素
count += min(n+1, nextRoot) - root
root *= 10
nextRoot *= 10
}
return count
}
// 从 1 开头的集合开始处理
prefix := 1
// 放个变量让循环循环使用
count := 0
for k > 1 {
// 求 prefix 为根的树元素(集合)的个数
count = getCount(prefix)
// k>=count 表明目标不在这个子树(集合)中,需要跳到下一个子树(集合),如 1=>2(11=>12)
// k==count+1时, 执行完 k-=count 会不满足循环
// 此时代表着结果是 下一个子树(集合)的第一个元素,也就是 2(或者12)
// 所以继续执行 prefix++ 没毛病
if k > count {
k -= count
prefix++
} else if k <= count {
// k<count 表明结果就在这个子树(集合)中,需要深入下一层分析,如 1=>10(11=>110)
// k==2 时, ,执行完 k-- 会不满足循环
// 代表此时结果就是 当前未处理的 prefix 子树元素(集合)中第二个元素,也就是 10(110)
k--
prefix *= 10
}
}
return prefix
}