刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/search-a-2d-matrix/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

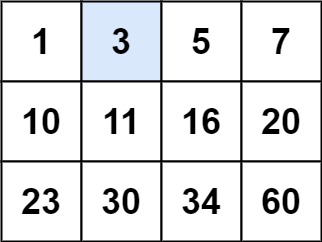
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

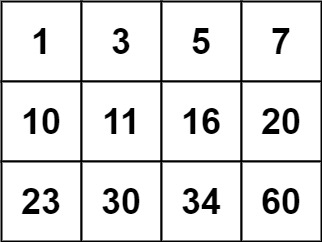
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -10^4 <= matrix[i][j], target <= 10^4

思路

这道题挺简单的，按题意其实就是

• 一个从左到右，从上到上整体递增的一个矩阵
• 从左到右过程中可能出现重复元素（非严格递增）
• 从上层到下层一定是递增的，下层头部元素大于上层尾部元素

在这样的矩阵里找是否存在，那就是分两步

• 找到可能存在的行
• 在可能存在行中找是否确实存在元素

没看到更多的提示和信息，两次二分即可

直接上代码~

代码

func searchMatrix(matrix [][]int, target int) bool {
	m, n := len(matrix), len(matrix[0])
    // 找可能存在的行
	iStart, iEnd := 0, m-1
	iTarget := -1
	for iEnd >= iStart {
		iMid := (iStart + iEnd) / 2
        // 找到直接返回
		if matrix[iMid][0] <= target && matrix[iMid][n-1] >= target {
			iTarget = iMid
			break
		}
		if target > matrix[iMid][n-1] {
			iStart = iMid + 1
		} else {
			iEnd = iMid - 1
		}
	}
    // 找不到可能存在的行就可以直接结束了
	if iTarget < 0 {
		return false
	}

    // 在可能存在的行里找元素
	jStart, jEnd := 0, n-1
	for jEnd >= jStart {
		jMid := (jStart + jEnd) / 2
		if matrix[iTarget][jMid] == target {
			return true
		}
		if target > matrix[iTarget][jMid] {
			jStart = jMid + 1
		} else {
			jEnd = jMid - 1
		}
	}
	return false
}