刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/delete-node-in-a-bst/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

• 首先找到需要删除的节点；
• 如果找到了，删除它。

示例 1:

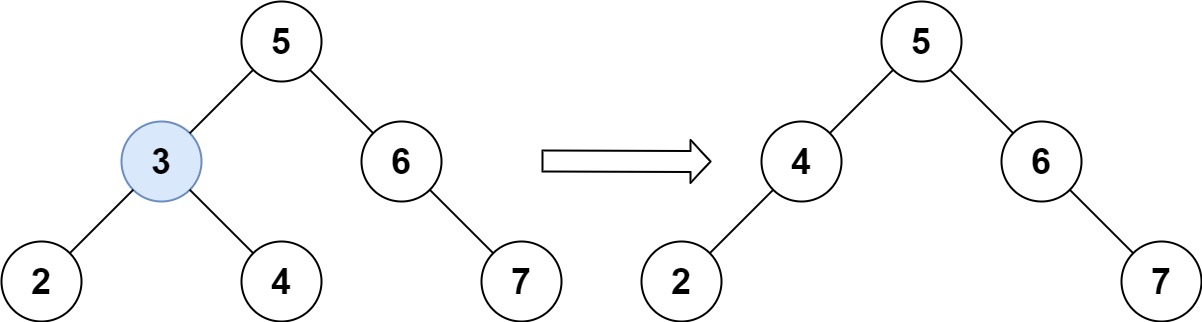
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

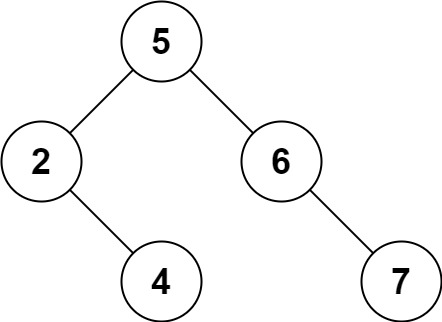
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 10^4].
• -10^5 <= Node.val <= 10^5
• 节点值唯一
• root 是合法的二叉搜索树
• -10^5 <= key <= 10^5

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

思路

二叉搜索树

首先，我们需要明确二叉搜索树的性质：

对于一个根节点来说，左子树的所有节点均小于根节点，右子树的所有节点均大于根节点

• 因为进阶要求的存在，我们需要利用这个性质来完成搜索
• 同时，也需要在搜索到目标节点后通过调整，使得删除节点后的树依然保持这个性质

解题思路

• 常规的二叉树搜索并不能在 O(h) 完成，但是二叉搜索树可以，因为对于每一次左右选择都是确定的
• 搜索很简单 ，关键就在于如何删除目标节点
• 删除后需要寻找一个节点来代替目标节点，要求就是需要满足替换后，左子树需要均小于新节点，右子树需要均大于新节点
  • 再挖细节，对于目标节点来说，没有左子树、没有右子树、没有左右子树这三种情况都很好处理，直接清理，让子节点替代即可，但是对于有左右子树的情况，就不能直接替换了，下面单独说明

有左右子树情况

首先是第一个问题，如何选择替换节点

因为要满足二叉搜索树的性质，所以我们有两个选择

• 左子树中的最大值
• 右子树中的最小值

如何替换

以去左子树找最大值为例，这里其实会有两种情况

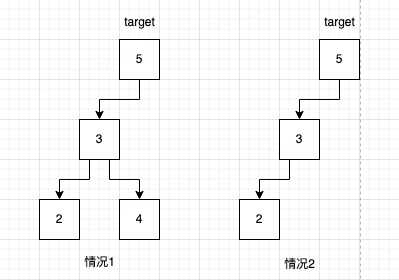
• 比较复杂的如图中情况1

比如目标节点是5节点，左子树最大值是4，其实这个时候，4节点一定没有右子树，因为如果存在，那么4就不是最大值， 而如果4节点有左子树，左子树的值也都大于3，因为这些节点都属于3节点的右子树。所以替换方法就是将4节点的左子树直接赋值到3节点的右子树即可

• 比较简单的如图中情况2

同样目标节点是5节点，此时3节点没有右子树，因为3节点的左子树中一定不会存在比3大的数字，所以3就是5节点左子树的最大值。因此只需要把3节点的左子树赋值到5节点的左子树即可

这里情况分析确实比较绕，可以画图多思考一下，至此上代码，细节在注释~

另有递归法可以去leetcode题解区看看~

代码

func deleteNode(root *TreeNode, key int) *TreeNode {
	if root == nil {
		return nil
	}

	var pre *TreeNode
	target := root
	// 没找到就继续找
	for target != nil && target.Val != key {
		// 记录前一个节点
		// 比当前节点大的数在右子树
		// 比当前节点小的数在左子树
		pre = target
		if target.Val > key {
			target = target.Left
		} else {
			target = target.Right
		}
	}

	// target 为空说明走到了叶子节点之后还是没找到，直接返回root
	if target == nil {
		return root
	}

	// 删除节点
	if target.Left == nil && target.Right == nil {
		target = nil
	} else if target.Left == nil {
		target = target.Right
	} else if target.Right == nil {
		target = target.Left
	} else {
		// 为了保证二叉搜索树
		// 找到左子树的最大值，替换target（找到右子树的最小值也可）
		leftMaxPre := target
		leftMax := target.Left
		for leftMax.Right != nil {
			leftMaxPre = leftMax
			leftMax = leftMax.Right
		}
		// 找到左子树最大值节点之后，有两种情况
		// 一种情况，其实左子树中根本没有右子树，此时最大值就是 target.Left 自身
		// 也就是 leftMaxPre == target 依然成立
		// 这里配图看比较清晰，此时直接将右子树接上，拿走 leftMax 替代 target 即可
		if leftMaxPre == target {
			leftMaxPre.Left = leftMax.Left
		} else {
			// 否则需要将 leftMax 的左子树接到 leftMaxPre 的右子树上
			// 因为此时 leftMax 在 leftMaxPre 的右子树
			// 但是 leftMax 已经没有了右子树，只剩下（或者可能也没有）左子树了
			leftMaxPre.Right = leftMax.Left
		}

		// 使用 leftMax 替换 target
		leftMax.Left = target.Left
		leftMax.Right = target.Right
		target = leftMax
	}

	// pre 为空则是找到了，但是就是root本身，直接返回 target
	if pre == nil {
		return target
	}

	// 判断target在pre的左子树还是子树
	if pre.Left != nil && pre.Left.Val == key {
		pre.Left = target
	} else {
		pre.Right = target
	}
	return root
}