刷题使我快乐,满脸开心.jpg
- 来源:力扣(LeetCode)
- 链接:https://leetcode.cn/problems/median-of-two-sorted-arrays/
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n))。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
思路
首先分享下我的思路:
- 因为有序,不用事先排序了。
- 起两个指针,初始都指向两个数组的起点
- 然后循环比较两者指针指向值大小,小的后移一位,其中一个数组为空则移动另一个数组指针
- 当移动
总个数/2下取整次数时,此时找到的数(总个数为奇数),或者找到的数和前一个数(总个数为偶数)即为中位数或者中位数两边的数,计算即可返回结果。
但是,最大的问题是,这样时间复杂度是O(m+n)。
如果要达到O(log(m+n)),那么就需要二分法。这里只说下思路具体分析参见官方题解~。
- 二分的思路来源于,将寻找中位数转变为找第
len/2个数(或者len/2和len/2-1) - 而在有序的前提下,可以两边各取
len/2个数的一半,而此位置中,比较小的一方及其元素其实是可以抛弃的,因为这些元素肯定是比比较大这一方的元素前面,如图中2,3两个元素
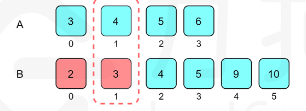
- 那么然后就是在截断一方数组的前提下,寻找两个新的数组中,第
len/2-x个数(x为刚才截取的元素个数) - 重复此步骤,直到一边数组为空,或者直到找两个数组中第一个数,那么就是返回更小的那一方即可
这个方法的代码下面贴了一份,详见官方题解
思路不难,难点在于边界,,,共勉吧。
至此,上代码
代码
遍历寻找中位数
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
m := len(nums1)
n := len(nums2)
p1, p2, left, right := 0, 0, 0, 0
for i := 0; i <= (m + n)/2; i++ {
left = right
if p1 < m && (p2 >= n || nums1[p1] < nums2[p2]) {
right = nums1[p1]
p1++
} else {
right = nums2[p2]
p2++
}
}
if (m + n)%2 == 0 {
return float64((left + right))/2
} else {
return float64(right)
}
}
二分法
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
totalLength := len(nums1) + len(nums2)
if totalLength%2 == 1 {
midIndex := totalLength/2
return float64(getKthElement(nums1, nums2, midIndex + 1))
} else {
midIndex1, midIndex2 := totalLength/2 - 1, totalLength/2
return float64(getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0
}
return 0
}
func getKthElement(nums1, nums2 []int, k int) int {
index1, index2 := 0, 0
for {
if index1 == len(nums1) {
return nums2[index2 + k - 1]
}
if index2 == len(nums2) {
return nums1[index1 + k - 1]
}
if k == 1 {
return min(nums1[index1], nums2[index2])
}
half := k/2
newIndex1 := min(index1 + half, len(nums1)) - 1
newIndex2 := min(index2 + half, len(nums2)) - 1
pivot1, pivot2 := nums1[newIndex1], nums2[newIndex2]
if pivot1 <= pivot2 {
k -= (newIndex1 - index1 + 1)
index1 = newIndex1 + 1
} else {
k -= (newIndex2 - index2 + 1)
index2 = newIndex2 + 1
}
}
return 0
}
func min(x, y int) int {
if x < y {
return x
}
return y
}
作者:力扣官方题解
链接:https://leetcode.cn/problems/median-of-two-sorted-arrays/solutions/258842/xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-s-114/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。