刷题使我快乐,满脸开心.jpg
- 来源:力扣(LeetCode)
- 链接:https://leetcode.cn/problems/minimum-cost-to-reach-destination-in-time/
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目
一个国家有 n 个城市,城市编号为 0 到 n - 1 ,题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组 edges 表示,其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路,耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路,但是不会有道路两头连接着同一座城市。
每次经过一个城市时,你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示,其中 passingFees[j] 是你经过城市 j 需要支付的费用。
一开始,你在城市 0 ,你想要在 maxTime 分钟以内 (包含 maxTime 分钟)到达城市 n - 1 。旅行的 费用 为你经过的所有城市 通行费之和 (包括 起点和终点城市的通行费)。
给你 maxTime,edges 和 passingFees ,请你返回完成旅行的 最小费用 ,如果无法在 maxTime 分钟以内完成旅行,请你返回 -1 。
示例 1:
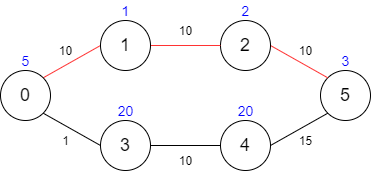
输入:maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出:11
解释:最优路径为 0 -> 1 -> 2 -> 5 ,总共需要耗费 30 分钟,需要支付 11 的通行费。
示例 2:
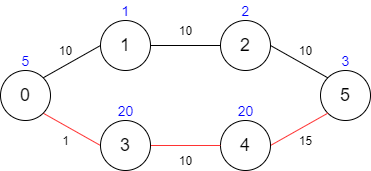
输入:maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出:48
解释:最优路径为 0 -> 3 -> 4 -> 5 ,总共需要耗费 26 分钟,需要支付 48 的通行费。
你不能选择路径 0 -> 1 -> 2 -> 5 ,因为这条路径耗费的时间太长。
示例 3:
输入:maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出:-1
解释:无法在 25 分钟以内从城市 0 到达城市 5 。
提示:
1 <= maxTime <= 1000n == passingFees.length2 <= n <= 1000n - 1 <= edges.length <= 10000 <= xi, yi <= n - 11 <= timei <= 10001 <= passingFees[j] <= 1000- 图中两个节点之间可能有多条路径。
- 图中不含有自环。
思路
最开始,我的思路是用dijkstra来解题,但是最终没有走通,暂时还没有找到问题,回头再论
用动规的话,这里最难的就是如何写出状态转移方程了,有两个维度,时间和费用,时间的限制是一个范围,而费用的要求是找最小,但是时间和费用并非存在直接联系,所以需要把时间和费用独立开,满足状态转移方程的无后效性。
与787题类似,这里可以将时间和到达点作为维度,费用作为点值,给出如下定义:
f[t][i] 表示,恰好t时间时,从点0到达点i的费用
代码
func minCost(maxTime int, edges [][]int, passingFees []int) int {
n := len(passingFees)
maxFee := 1000*1000 + 1
// cost[a][b] 表示恰好在a时间时从0到b,此时值为其花费
cost := make([][]int, maxTime+1)
for i := 0; i < maxTime+1; i++ {
cost[i] = make([]int, n)
for j := 0; j <= n-1; j++ {
cost[i][j] = maxFee
}
}
cost[0][0] = passingFees[0]
for nowTime := 1; nowTime <= maxTime; nowTime++ {
for _, edge := range edges {
from, to, timeCost := edge[0], edge[1], edge[2]
if nowTime >= edge[2] {
// 费用确定值是在0时间0位置的点,所以需要从0点出发算其他点
cost[nowTime][to] = min(cost[nowTime][to], cost[nowTime-timeCost][from]+passingFees[to])
cost[nowTime][from] = min(cost[nowTime][from], cost[nowTime-timeCost][to]+passingFees[from])
}
}
}
minCostFee := maxFee
for costTime := 1; costTime <= maxTime; costTime++ {
minCostFee = min(minCostFee, cost[costTime][n-1])
}
if minCostFee >= maxFee {
return -1
}
return minCostFee
}
func min(a, b int) int {
if a > b {
return b
}
return a
}