刷题使我快乐,满脸开心.jpg
- 来源:力扣(LeetCode)
- 链接:https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/
- 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题目
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums中的所有整数 互不相同nums原来是一个升序排序的数组,并进行了1至n次旋转
思路
二分法
明显的提示,用二分
这里传统的二分可能会陷入思维陷阱,因为传统二分,用边界做基准,此时因为基准的不断变化,会导致思路难度飙升,感觉就算可以解答也会非常复杂
基准
那就找个基准
其实很容易找到,那就是数组中位置 0和len(nums)-1。理论上都可以,但是这里我更推荐0
因为基准如果恰好是最小值,感觉上会增加思维的复杂度(其实并不一定,但是我本人喜欢剥离开思考问题)
而0如果是最小值,恰好是一个特殊情况,恰好旋转回了原始数组,只有此种情况下:
nums[0] <= nums[len(nums)-1]
等于是只有一个元素的情况
二分思路
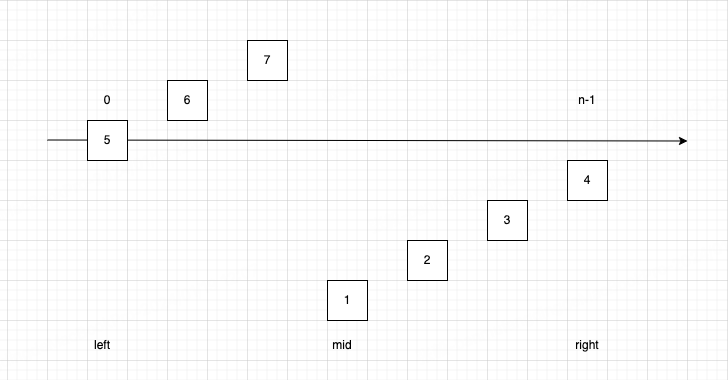
放个图辅助说明,二分思路其实很简单,因为除了上述特殊情况下
- 如果
nums[mid] >= nums[0],那最小值一定在右边 - 如果
nums[mid] < nums[0],那最小值一定在左边
特殊情况
那肯定有人会担心,如果恰好mid在最小值怎么办,上面的判断不成立了啊!
不用担心,我们用外循环的一个小技巧就能覆盖住
正常来讲,二分法的外循环根据不同题目,会是 left < right 或者 left <= right,但是这道题我的思路下必须用 left <= right
因为在如图中,
mid恰好在最小值的情况下,区间会走到左边
此时区间内所有数字都比nums[0]大,所以会不断累加left,直到left = right + 1退出
而此时,也就恰好覆盖住了特殊的情况,找到了右边界右边的这个最小值
OK,思路基本就说完了,老样子,细节在代码注释了~
代码
func findMin(nums []int) int {
left, right := 0, len(nums)-1
// 特殊情况
if nums[left] < nums[right] {
return nums[0]
}
// 一般情况,二分查找
mid := 0
for left <= right {
mid = left + (right-left)/2
// 这里以nums[0]为基准
// 如果还用left为基准的话,因为left位置的不确定性
// 会难以判断应该往哪个方向走
if nums[mid] >= nums[0] {
left = mid + 1
} else {
right = mid - 1
}
}
// 不需要担心恰好mid在最小值的情况
// 因为那样会导致区间一直往right靠近
// 最终发现right还是大于nums[0]
// 使得 left=right+1 不满足left<=right退出
// 此时left恰好是最小值了
return nums[left]
}