刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/search-a-2d-matrix-ii/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例 1：

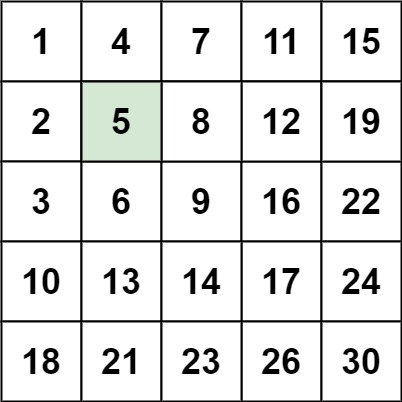
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

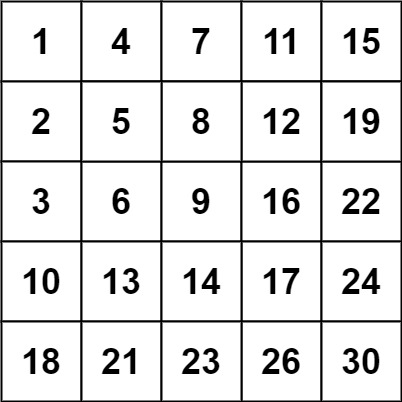
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -109 <= matrix[i][j] <= 109
• 每行的所有元素从左到右升序排列
• 每列的所有元素从上到下升序排列
• -109 <= target <= 109

思路

第一反应是二分法，但是看着题目中高效那两个字，总觉得很是扎眼，所以感觉对于一个矩阵来说，总归应该有些更高效的才对。

思路如下:

• 数据顺序是有两个方向的，横向和纵向，那么理论上我们是能够通过一个点来排除两个方向上的数据的，但是打个比方，发现[i][j]点的值比target小，我们能够排除比这个点左边和上边的所有数据，但是接下来我们是往右移动还是往左移动呢？感觉这个问题其实也比较复杂，那有没有没有歧义的移动方法呢？
• 然后就发现在这个矩阵中会有两个特殊的点，左下角和右下角，特殊之处在于，比这两个点大的方向和比这俩个点小的数据，都只有一个方向。这有一个方向，那么就没有歧义了，所以移动起来就只会有一种选择！

如图展示下寻找步骤：
灰色部分被淘汰的数据

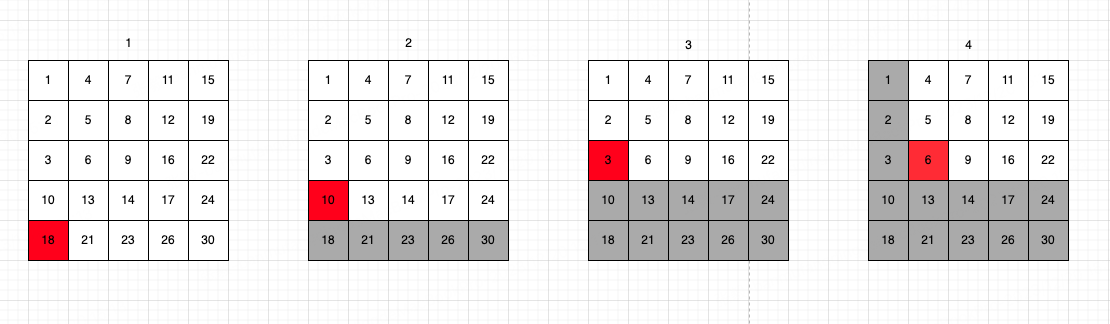
如此，每次判断都可以pass掉一行或者一列数据，而在寻找过程中，当前点位也始终会保持在左下角或右下角这个特殊位置上

至此，上代码

代码

二分法

func searchMatrix(matrix [][]int, target int) bool {
    for _, row := range matrix {
        // 逐层搜索
        if binarySearch(row, target) {
            return true
        }
    }
    return false
}

// 二分法
func binarySearch(nums []int, target int) bool {
    n := len(nums)
    if target > nums[n-1] || target < nums[0] {
        return false
    }
    if target == nums[n-1] || target == nums[0] {
        return true
    }
    left, right, mid := 0, n-1, 0
    for left <= right {
        mid = (left + right) / 2
        if nums[mid] == target {
            return true
        } else if target > nums[mid] {
            left = mid + 1
        } else {
            right = mid - 1
        }
    }
    return false
}

z字形查找（官解名）

func searchMatrix(matrix [][]int, target int) bool {
    m := len(matrix)
    n := len(matrix[0])
    i, j := m-1, 0
    for i >= 0 && j < n  {
        if matrix[i][j] == target {
            return true
        } else if matrix[i][j] > target {
            i--
        } else {
            j++
        }
    }
    return false
}