刷题使我快乐，满脸开心.jpg

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/unique-paths/
• 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

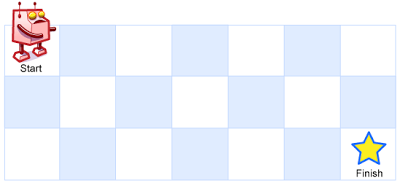
问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

思路

典型动态规划题了，这里简单说下：

dp定义

dp[i][j] 含义为从 [i，j] 坐标去往终点的路径数量

状态转移方程

路径数量为从下方过来的路径数 加上 从右边过来的路径数之和

dp[i][j] = dp[i+1][j] + dp[i][j+1]

初始数据

只能从右方和下方过来，所以最右边一列只能从下放过来、最下方一排只能从右边过来，所以路径数都是1。

代码也基本就出来了。老样子，细节在代码注释

代码

func uniquePaths(m int, n int) int {
	// dp[i][j] 含义为从从i，j坐标去往终点的路径数量
	dp := make([][]int, m)
	for mk, _ := range dp {
		dp[mk] = make([]int, n)
        // 最后一排数据初始化
		if mk == m-1 {
			for nk, _ := range dp[mk] {
				dp[mk][nk] = 1
			}
		}
        // 最后一列数据初始化
		dp[mk][n-1] = 1
	}
	for i := m - 2; i >= 0; i-- {
		for j := n - 2; j >= 0; j-- {
			dp[i][j] = dp[i+1][j] + dp[i][j+1]
		}
	}
	return dp[0][0]
}